晴天有时候下猪

分布的分布：我们假设一个数据集，这个数据集是由许多个同类分布得到的点共同组成的，现在有一个点，需要知道这个点满足其中某一个分布的概率
狄利克雷过程（dirichlet process ）：
原始定义：
假设存在在度量空间\Theta上的分布H和一个参数\alpha，如果对于度量空间\Theta的任意一个可数划分（可以是有限或者无限的）A1, A2,...,An，都有下列式子成立：
(G(A1),G(A2),...,G(An)) ~ Dir(\alpha H(A1), \alpha H(A2),..., \alpha H(An)),  这里Dir是dirichlet 分布，我们称G是满足Dirichlet process的。这个定义是1973年Ferguson最早提出的定义。
In probability theory, Dirichlet processes (after Peter Gustav Lejeune Dirichlet) are a family of stochastic processes whose realizations are probability distributions. In other words, a Dirichlet process is a probability distribution whose domain is itself a set of probability distributions.
The Dirichlet process is specified by a base distribution 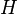and a positive real number called the concentration parameter. The base distribution is the expected value of the process, that is, the Dirichlet process draws distributions "around" the base distribution in the way that a normal distribution draws real numbers around its mean. However, even if the base distribution iscontinuous, the distributions drawn from the Dirichlet process are almost surely discrete. The concentration parameter specifies how strong this discretization is: in the limit of , the realizations are all concentrated on a single value, while in the limit of the realizations become continuous. In between the two extremes the realizations are discrete distributions with less and less concentration as increases.
The Dirichlet process can also be seen as the infinite-dimensional generalization of the Dirichlet distribution. In the same way as the Dirichlet distribution is the conjugate prior for thecategorical distribution, the Dirichlet process is the conjugate prior for infinite, nonparametric discrete distributions. A particularly important application of Dirichlet processes is as aprior probability distribution in infinite mixture models.（From wiki:https://en.wikipedia.org/wiki/Dirichlet_process）
按照我个人的理解就是一个分类过程，这个过程中每加入一个新的样本有两种可能性，第一种可能性为加入的这个样本属于前面已经分好的类中，第二种为新加入的样本不能分到前面任何一类当中，
 
对于一个已知由高斯混合模型生成的数据集：

虽然已知由高斯混合模型生成了此数据集，但是并不知道高斯混合模型的个数，不知道是由多少个高斯混合模型生成了上述数据集。对于这样的情况我们怎么做呢？1.可以使用EM方法选择1、2、3…个高斯模型进行拟合取最好的结果2.可以使用层次聚类得到层次聚类树，然后通过目视进行判断等等方法。然而实际上我们希望使用统计的方法进行分类，而不需要进行使用其他的技巧
Eq(1)

Polya urn模型：
假设我们有一个缸，里面没有球，现在我们从一个分布H中选取一种颜色，然后把这种颜色涂在一个球上放入缸中；然后我们要么从缸中抽取一个球出来，然后再放入两个和这个球同种颜色的球进入缸中；要么就从分布H中选取一个颜色，然后把这种颜色涂在一个球上放入缸中。从缸中抽取某种颜色的一个球的概率是ni/(\alpha+n)，ni是这种颜色的球的个数，n是总的球个数；不从缸中抽取而放入一种颜色的球的概率是\alpha/(\alpha+n)。很明显，polya urn模型和CRP有一一对应的关系，颜色对应一个桌子，坐新桌子对应于不从缸中选取而是从H中选取一种颜色涂球放入缸中。
stick-breaking模型：
假设有一个长度为1的线段，我们从中选取\pi_1长出来，剩下的部分再选取\pi_2出来，循环下去，\pi_n，无穷下去，这个有点类似我们古代的一句话：
“一尺之踵，日取其半，万世不竭”，它们满足\sum \pi_i ＝ 1
对每个\pi_i，我们都从分布H中选取一个\theta_i，然后从F(\theta_i)中选取出一个x_i出来。这里的\theta_i就对应一个cluster，类似地，我们可以看到数据自然地被分为了各个堆，可以证明这个模型仍然是一个DP。
模型公式如下：

上述描述中pi_i类似于公式中的vi，vi的获取是通过Beta函数获取的为一个函数，其中属于则值为1，否则值为0，这样可以得到G函数，G函数满足dirichlet分布，由上述过程可以知道stick breaking的过程。
 
无限混合模型：
从stick－breaking模型我们看出，我们可以把DP看着是一个无限混合模型，即
G ~ \sum_1^\inf \pi_i*F(\theta_i)，其中\sum \pi_i ＝ 1。\pi_i 就是混合模型中每个子模型的权重。
目前应用最多的还是从第五种角度来看待问题，即把DP看着是一个无限混合模型，其中值得注意的是：
1）虽然DP是一个无限混合模型，但是可以证明，随着数据的增多，模型的个数是呈现log 增加的，即模型的个数的增长是比数据的增长要缓慢得多的；
2）DP是有一个马太效应在里面的，即越富裕的人越来越富裕，我们可以从第二和第三种解释中看到，每个桌子或者颜色已经有的数据越多，那么下一次被选中的概率越大，因为是与在桌子上的个数成正比的。
非参贝叶斯
之前研究过一段时间的非参贝叶斯，但是对为什么叫“非参”，以及dirichlet process不是很了解，今天看到一篇神文，深入浅出的娓娓道来
为什么叫“非参”：传统的聚类在开始的时候就要设定类别的数目，而“非参”是指随着数据的不断增加，新的类别不断加入
这篇神文更是简历了 餐厅问题和 dirichlet process 的关系
转自：http://blog.echen.me/
转自：http://blog.csdn.net/sunmenggmail/article/details/7429756
Imagine you’re a budding chef. A data-curious one, of course, so you start by taking a set of foods (pizza, salad, spaghetti, etc.) and ask 10 friends how much of each they ate in the past day.
Your goal: to find natural groups of foodies, so that you can better cater to each cluster’s tastes. For example, your fratboy friends might love wings and beer, your anime friends might love soba and sushi, your hipster friends probably dig tofu, and so on.
So how can you use the data you’ve gathered to discover different kinds of groups?

One way is to use a standard clustering algorithm like k-means or Gaussian mixture modeling(see this previous post for a brief introduction). The problem is that these both assume a fixed number of clusters, which they need to be told to find. There are a couple methods for selecting the number of clusters to learn (e.g., the gap and prediction strength statistics), but the problem is a more fundamental one: most real-world data simply doesn’t have a fixed number of clusters.
That is, suppose we’ve asked 10 of our friends what they ate in the past day, and we want to find groups of eating preferences. There’s really an infinite number of foodie types (carnivore, vegan, snacker, Italian, healthy, fast food, heavy eaters, light eaters, and so on), but with only 10 friends, we simply don’t have enough data to detect them all. (Indeed, we’re limited to 10 clusters!) So whereas k-means starts with the incorrect assumption that there’s a fixed, finite number of clusters that our points come from, no matter if we feed it more data, what we’d really like is a method positing an infinite number of hidden clusters that naturally arise as we ask more friends about their food habits. (For example, with only 2 data points, we might not be able to tell the difference between vegans and vegetarians, but with 200 data points, we probably could.)
Luckily for us, this is precisely the purview of nonparametric Bayes.*
*Nonparametric Bayes refers to a class of techniques that allow some parameters to change with the data. In our case, for example, instead of fixing the number of clusters to be discovered, we allow it to grow as more data comes in.

A Generative Story

Let’s describe a generative model for finding clusters in any set of data. We assume an infinite set of latent groups, where each group is described by some set of parameters. For example, each group could be a Gaussian with a specified mean μi and standard deviation σi, and these group parameters themselves are assumed to come from some base distribution G0. Data is then generated in the following manner:

• Select a cluster.
• Sample from that cluster to generate a new point.

(Note the resemblance to a finite mixture model.)
For example, suppose we ask 10 friends how many calories of pizza, salad, and rice they ate yesterday. Our groups could be:

• A Gaussian centered at (pizza = 5000, salad = 100, rice = 500) (i.e., a pizza lovers group).
• A Gaussian centered at (pizza = 100, salad = 3000, rice = 1000) (maybe a vegan group).
• A Gaussian centered at (pizza = 100, salad = 100, rice = 10000) (definitely Asian).
• …

When deciding what to eat when she woke up yesterday, Alice could have thought girl, I’m in the mood for pizza and her food consumption yesterday would have been a sample from the pizza Gaussian. Similarly, Bob could have spent the day in Chinatown, thereby sampling from the Asian Gaussian for his day’s meals. And so on.
The big question, then, is: how do we assign each friend to a group?

Assigning Groups

Chinese Restaurant Process

One way to assign friends to groups is to use a Chinese Restaurant Process. This works as follows: Imagine a restaurant where all your friends went to eat yesterday…

• Initially the restaurant is empty.
• The first person to enter (Alice) sits down at a table (selects a group). She then orders food for the table (i.e., she selects parameters for the group); everyone else who joins the table will then be limited to eating from the food she ordered.
• The second person to enter (Bob) sits down at a table. Which table does he sit at? With probability α/(1+α) he sits down at a new table (i.e., selects a new group) and orders food for the table; with probability 1/(1+α) he sits with Alice and eats from the food she’s already ordered (i.e., he’s in the same group as Alice).
• …
• The (n+1)-st person sits down at a new table with probability α/(n+α), and at table k with probability nk/(n+α), where nk is the number of people currently sitting at table k.

Note a couple things:

• The more people (data points) there are at a table (cluster), the more likely it is that people (new data points) will join it. In other words, our groups satisfy a rich get richer property.
• There’s always a small probability that someone joins an entirely new table (i.e., a new group is formed).
• The probability of a new group depends on α. So we can think of α as a dispersion parameter that affects the dispersion of our datapoints. The lower alpha is, the more tightly clustered our data points; the higher it is, the more clusters we have in any finite set of points.

(Also notice the resemblance between table selection probabilities and a Dirichlet distribution…)
Just to summarize, given n data points, the Chinese Restaurant Process specifies a distribution over partitions (table assignments) of these points. We can also generate parameters for each partition/table from a base distribution G0 (for example, each table could represent a Gaussian whose mean and standard deviation are sampled from G0), though to be clear, this is not part of the CRP itself.

Code

Since code makes everything better, here’s some Ruby to simulate a CRP:
Chinese Restaurant Processchinese_restaurant_process.rb

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# Generate table assignments for `num_customers` customers, according to
# a Chinese Restaurant Process with dispersion parameter `alpha`.
#
# returns an array of integer table assignments
def chinese_restaurant_process(num_customers, alpha)
 return [] if num_customers <= 0

 table_assignments = [1] # first customer sits at table 1
 next_open_table = 2 # index of the next empty table

 # Now generate table assignments for the rest of the customers.
 1.upto(num_customers - 1) do |i|
   if rand < alpha.to_f / (alpha + i)
     # Customer sits at new table.
     table_assignments << next_open_table
     next_open_table += 1
   else
     # Customer sits at an existing table.
     # He chooses which table to sit at by giving equal weight to each
     # customer already sitting at a table. 
     which_table = table_assignments[rand(table_assignments.size)]
     table_assignments << which_table
   end
 end

 table_assignments
end

And here’s some sample output:
Chinese Restaurant Processchinese_restaurant_process.rb

1
2
3
4
5
6
7
8
9
10
11
12
13
14

> chinese_restaurant_process(num_customers = 10, alpha = 1)
1, 2, 3, 4, 3, 3, 2, 1, 4, 3 # table assignments from run 1
1, 1, 1, 1, 1, 1, 2, 2, 1, 3 # table assignments from run 2
1, 2, 2, 1, 3, 3, 2, 1, 3, 4 # table assignments from run 3

> chinese_restaurant_process(num_customers = 10, alpha = 3)
1, 2, 1, 1, 3, 1, 2, 3, 4, 5
1, 2, 3, 3, 4, 3, 4, 4, 5, 5
1, 1, 2, 3, 1, 4, 4, 3, 1, 1

> chinese_restaurant_process(num_customers = 10, alpha = 5)
1, 2, 1, 3, 4, 5, 6, 7, 1, 8
1, 2, 3, 3, 4, 5, 6, 5, 6, 7
1, 2, 3, 4, 5, 6, 2, 7, 2, 1

Notice that as we increase α, so too does the number of distinct tables increase.

Polya Urn Model

Another method for assigning friends to groups is to follow the Polya Urn Model. This is basically the same model as the Chinese Restaurant Process, just with a different metaphor.

• We start with an urn containing αG0(x) balls of “color” x, for each possible value of x. (G0 is our base distribution, and G0(x) is the probability of sampling x from G0). Note that these are possibly fractional balls.
• At each time step, draw a ball from the urn, note its color, and then drop both the original ball plus a new ball of the same color back into the urn.

Note the connection between this process and the CRP: balls correspond to people (i.e., data points), colors correspond to table assignments (i.e., clusters), alpha is again a dispersion parameter (put differently, a prior), colors satisfy a rich-get-richer property (since colors with many balls are more likely to get drawn), and so on. (Again, there’s also a connection between this urn model and the urn model for the (finite) Dirichlet distribution…)
To be precise, the difference between the CRP and the Polya Urn Model is that the CRP specifies only a distribution over partitions (i.e., table assignments), but doesn’t assign parameters to each group, whereas the Polya Urn Model does both.

Code

Again, here’s some code for simulating a Polya Urn Model:
Polya Urn Modelpolya_urn_model.rb

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# Draw `num_balls` colored balls according to a Polya Urn Model
# with a specified base color distribution and dispersion parameter
# `alpha`.
#
# returns an array of ball colors
def polya_urn_model(base_color_distribution, num_balls, alpha)
  return [] if num_balls <= 0

  balls_in_urn = []
  0.upto(num_balls - 1) do |i|
    if rand < alpha.to_f / (alpha + balls_in_urn.size)
      # Draw a new color, put a ball of this color in the urn.
      new_color = base_color_distribution.call
      balls_in_urn << new_color
    else
      # Draw a ball from the urn, add another ball of the same color.
      ball = balls_in_urn[rand(balls_in_urn.size)]
      balls_in_urn << ball
    end
  end

  balls_in_urn
end

And here’s some sample output, using a uniform distribution over the unit interval as the color distribution to sample from:
Polya Urn Modelpolya_urn_model.rb

1
2
3
4
5
6

> unit_uniform = lambda { (rand * 100).to_i / 100.0 }

> polya_urn_model(unit_uniform, num_balls = 10, alpha = 1)
0.27, 0.89, 0.89, 0.89, 0.73, 0.98, 0.43, 0.98, 0.89, 0.53 # colors in the urn from run 1
0.26, 0.26, 0.46, 0.26, 0.26, 0.26, 0.26, 0.26, 0.26, 0.85 # colors in the urn from run 2
0.96, 0.87, 0.96, 0.87, 0.96, 0.96, 0.87, 0.96, 0.96, 0.96 # colors in the urn from run 3

Code, Take 2

Here’s the same code for a Polya Urn Model, but in R:
Polya Urn Modelpolya_urn_model.R

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# Return a vector of `num_balls` ball colors according to a Polya Urn Model
# with dispersion `alpha`, sampling from a specified base color distribution.
polya_urn_model = function(base_color_distribution, num_balls, alpha) {
  balls = c()

  for (i in 1:num_balls) {
    if (runif(1) < alpha / (alpha + length(balls))) {
      # Add a new ball color.
      new_color = base_color_distribution()
      balls = c(balls, new_color)
    } else {
      # Pick out a ball from the urn, and add back a
      # ball of the same color.
      ball = balls[sample(1:length(balls), 1)]
      balls = c(balls, ball)
    }
  }

  balls
}

Here are some sample density plots of the colors in the urn, when using a unit normal as the base color distribution:




Notice that as alpha increases (i.e., we sample more new ball colors from our base; i.e., as we place more weight on our prior), the colors in the urn tend to a unit normal (our base color distribution).
And here are some sample plots of points generated by the urn, for varying values of alpha:

• Each color in the urn is sampled from a uniform distribution over [0,10]x[0,10] (i.e., a [0, 10] square).
• Each group is a Gaussian with standard deviation 0.1 and mean equal to its associated color, and these Gaussian groups generate points.

Notice that the points clump together in fewer clusters for low values of alpha, but become more dispersed as alpha increases.

Stick-Breaking Process

Imagine running either the Chinese Restaurant Process or the Polya Urn Model without stop. For each group i, this gives a proportion wi of points that fall into group i.
So instead of running the CRP or Polya Urn model to figure out these proportions, can we simply generate them directly?
This is exactly what the Stick-Breaking Process does:

• Start with a stick of length one.
• Generate a random variable β1∼Beta(1,α). By the definition of the Beta distribution, this will be a real number between 0 and 1, with expected value 1/(1+α). Break off the stick at β1; w1 is then the length of the stick on the left.
• Now take the stick to the right, and generate β2∼Beta(1,α). Break off the stick β2 into the stick. Again, w2 is the length of the stick to the left, i.e., w2=(1−β1)β2.
• And so on.

Thus, the Stick-Breaking process is simply the CRP or Polya Urn Model from a different point of view. For example, assigning customers to table 1 according to the Chinese Restaurant Process is equivalent to assigning customers to table 1 with probability w1.

Code

Here’s some R code for simulating a Stick-Breaking process:
Stick-Breaking Processstick_breaking_process.R

1
2
3
4
5
6
7
8
9
10
11
12
13

# Return a vector of weights drawn from a stick-breaking process
# with dispersion `alpha`.
#
# Recall that the kth weight is
#   \beta_k = (1 - \beta_1) * (1 - \beta_2) * ... * (1 - \beta_{k-1}) * beta_k
# where each $\\beta\_i$ is drawn from a Beta distribution
#   \beta_i ~ Beta(1, \alpha)
stick_breaking_process = function(num_weights, alpha) {
  betas = rbeta(num_weights, 1, alpha)
  remaining_stick_lengths = c(1, cumprod(1 - betas))[1:num_weights]
  weights = remaining_stick_lengths * betas
  weights
}

And here’s some sample output:



Notice that for low values of alpha, the stick weights are concentrated on the first few weights (meaning our data points are concentrated on a few clusters), while the weights become more evenly dispersed as we increase alpha (meaning we posit more clusters in our data points).

Dirichlet Process

Suppose we run a Polya Urn Model several times, where we sample colors from a base distribution G0. Each run produces a distribution of colors in the urn (say, 5% blue balls, 3% red balls, 2% pink balls, etc.), and the distribution will be different each time (for example, 5% blue balls in run 1, but 1% blue balls in run 2).
For example, let’s look again at the plots from above, where I generated samples from a Polya Urn Model with the standard unit normal as the base distribution:




Each run of the Polya Urn Model produces a slighly different distribution, though each is “centered” in some fashion around the standard Gaussian I used as base. In other words, the Polya Urn Model gives us a distribution over distributions (we get a distribution of ball colors, and this distribution of colors changes each time) – and so we finally get to the Dirichlet Process.
Formally, given a base distribution G0 and a dispersion parameter α, a sample from the Dirichlet Process DP(G0,α) is a distribution G∼DP(G0,α). This sample G can be thought of as a distribution of colors in a single simulation of the Polya Urn Model; sampling from G gives us the balls in the urn.
So here’s the connection between the Chinese Restaurant Process, the Polya Urn Model, the Stick-Breaking Process, and the Dirichlet Process:

• Dirichlet Process: Suppose we want samples xi∼G, where G is a distribution sampled from the Dirichlet Process G∼DP(G0,α).
• Polya Urn Model: One way to generate these values xi would be to take a Polya Urn Model with color distribution G0 and dispersion α. (xi would be the color of the ith ball in the urn.)
• Chinese Restaurant Process: Another way to generate xi would be to first assign tables to customers according to a Chinese Restaurant Process with dispersion α. Every customer at the nth table would then be given the same value (color) sampled from G0. (xi would be the value given to the ith customer; xi can also be thought of as the food at table i, or as the parameters of table i.)
• Stick-Breaking Process: Finally, we could generate weights wk according to a Stick-Breaking Process with dispersion α. Next, we would give each weight wk a value (or color) vk sampled from G0. Finally, we would assign xi to value (color) vk with probability wk.

Recap

Let’s summarize what we’ve discussed so far.
We have a bunch of data points pi that we want to cluster, and we’ve described four essentially equivalent generative models that allow us to describe how each cluster and point could have arisen.
In the Chinese Restaurant Process:

• We generate table assignments g1,…,gn∼CRP(α) according to a Chinese Restaurant Process. (gi is the table assigned to datapoint i.)
• We generate table parameters ϕ1,…,ϕn∼G0 according to the base distribution G0, where ϕk is the parameter for the kth distinct group.
• Given table assignments and table parameters, we generate each datapoint pi∼F(ϕgi) from a distribution F with the specified table parameters. (For example, F could be a Gaussian, andϕi could be a parameter vector specifying the mean and standard deviation).

In the Polya Urn Model:

• We generate colors ϕ1,…,ϕn∼Polya(G0,α) according to a Polya Urn Model. (ϕi is the color of the ith ball.)
• Given ball colors, we generate each datapoint pi∼F(ϕi).

In the Stick-Breaking Process:

• We generate group probabilities (stick lengths) w1,…,w∞∼Stick(α) according to a Stick-Breaking process.
• We generate group parameters ϕ1,…,ϕ∞∼G0 from G0, where ϕk is the parameter for the kth distinct group.
• We generate group assignments g1,…,gn∼Multinomial(w1,…,w∞) for each datapoint.
• Given group assignments and group parameters, we generate each datapoint pi∼F(ϕgi).

In the Dirichlet Process:

• We generate a distribution G∼DP(G0,α) from a Dirichlet Process with base distribution G0 and dispersion parameter α.
• We generate group-level parameters xi∼G from G, where xi is the group parameter for the ith datapoint. (Note: this is not the same as ϕi. xi is the parameter associated to the group that the ith datapoint belongs to, whereas ϕk is the parameter of the kth distinct group.)
• Given group-level parameters xi, we generate each datapoint pi∼F(xi).

Also, remember that each model naturally allows the number of clusters to grow as more points come in.

Inference in the Dirichlet Process Mixture

So we’ve described a generative model that allows us to calculate the probability of any particular set of group assignments to data points, but we haven’t described how to actually learn a good set of group assignments.
Let’s briefly do this now. Very roughly, the Gibbs sampling approach works as follows:

• Take the set of data points, and randomly initialize group assignments.
• Pick a point. Fix the group assignments of all the other points, and assign the chosen point a new group (which can be either an existing cluster or a new cluster) with a CRP-ish probability (as described in the models above) that depends on the group assignments and values of all the other points.
• We will eventually converge on a good set of group assignments, so repeat the previous step until happy.

For more details, this paper provides a good description. Philip Resnick and Eric Hardisty also have a friendlier, more general description of Gibbs sampling (plus an application to naive Bayes) here.

Fast Food Application: Clustering the McDonald’s Menu

Finally, let’s show an application of the Dirichlet Process Mixture. Unfortunately, I didn’t have a data set of people’s food habits offhand, so instead I took this list of McDonald’s foods and nutrition facts.
After normalizing each item to have an equal number of calories, and representing each item as a vector of (total fat, cholesterol, sodium, dietary fiber, sugars, protein, vitamin A, vitamin C, calcium, iron, calories from fat, satured fat, trans fat, carbohydrates), I ran scikit-learn’s Dirichlet Process Gaussian Mixture Model to cluster McDonald’s menu based on nutritional value.
First, how does the number of clusters inferred by the Dirichlet Process mixture vary as we feed in more (randomly ordered) points?

As expected, the Dirichlet Process model discovers more and more clusters as more and more food items arrive. (And indeed, the number of clusters appears to grow logarithmically, which can in fact be proved.)
How many clusters does the mixture model infer from the entire dataset? Running the Gibbs sampler several times, we find that the number of clusters tends around 11:

Let’s dive into one of these clusterings.
Cluster 1 (Desserts)
Looking at a sample of foods from the first cluster, we find a lot of desserts and dessert-y drinks:

• Caramel Mocha
• Frappe Caramel
• Iced Hazelnut Latte
• Iced Coffee
• Strawberry Triple Thick Shake
• Snack Size McFlurry
• Hot Caramel Sundae
• Baked Hot Apple Pie
• Cinnamon Melts
• Kiddie Cone
• Strawberry Sundae

We can also look at the nutritional profile of some foods from this cluster (after z-scaling each nutrition dimension to have mean 0 and standard deviation 1):

We see that foods in this cluster tend to be high in trans fat and low in vitamins, protein, fiber, and sodium.
Cluster 2 (Sauces)
Here’s a sample from the second cluster, which contains a lot of sauces:

• Hot Mustard Sauce
• Spicy Buffalo Sauce
• Newman’s Own Low Fat Balsamic Vinaigrette

And looking at the nutritional profile of points in this cluster, we see that it’s heavy in sodium and fat:

Cluster 3 (Burgers, Crispy Foods, High-Cholesterol)
The third cluster is very burgery:

• Hamburger
• Cheeseburger
• Filet-O-Fish
• Quarter Pounder with Cheese
• Premium Grilled Chicken Club Sandwich
• Ranch Snack Wrap
• Premium Asian Salad with Crispy Chicken
• Butter Garlic Croutons
• Sausage McMuffin
• Sausage McGriddles

It’s also high in fat and sodium, and low in carbs and sugar

Cluster 4 (Creamy Sauces)
Interestingly, even though we already found a cluster of sauces above, we discover another one as well. These sauces appear to be much more cream-based:

• Creamy Ranch Sauce
• Newman’s Own Creamy Caesar Dressing
• Coffee Cream
• Iced Coffee with Sugar Free Vanilla Syrup

Nutritionally, these sauces are higher in calories from fat, and much lower in sodium:

Cluster 5 (Salads)
Here’s a salad cluster. A lot of salads also appeared in the third cluster (along with hamburgers and McMuffins), but that’s because those salads also all contained crispy chicken. The salads in this cluster are either crisp-free or have their chicken grilled instead:

• Premium Southwest Salad with Grilled Chicken
• Premium Caesar Salad with Grilled Chicken
• Side Salad
• Premium Asian Salad without Chicken
• Premium Bacon Ranch Salad without Chicken

This is reflected in the higher content of iron, vitamin A, and fiber:

Cluster 6 (More Sauces)
Again, we find another cluster of sauces:

• Ketchup Packet
• Barbeque Sauce
• Chipotle Barbeque Sauce

These are still high in sodium, but much lower in fat compared to the other sauce clusters:

Cluster 7 (Fruit and Maple Oatmeal)
Amusingly, fruit and maple oatmeal is in a cluster by itself:

• Fruit & Maple Oatmeal

Cluster 8 (Sugary Drinks)
We also get a cluster of sugary drinks:

• Strawberry Banana Smoothie
• Wild Berry Smoothie
• Iced Nonfat Vanilla Latte
• Nonfat Hazelnut
• Nonfat Vanilla Cappuccino
• Nonfat Caramel Cappuccino
• Sweet Tea
• Frozen Strawberry Lemonade
• Coca-Cola
• Minute Maid Orange Juice

In addition to high sugar content, this cluster is also high in carbohydrates and calcium, and low in fat.

Cluster 9 (Breakfast Foods)
Here’s a cluster of high-cholesterol breakfast foods:

• Sausage McMuffin with Egg
• Sausage Burrito
• Egg McMuffin
• Bacon, Egg & Chees Biscuit
• McSkillet Burrito with Sausage
• Big Breakfast with Hotcakes

Cluster 10 (Coffee Drinks)
We find a group of coffee drinks next:

• Nonfat Cappuccino
• Nonfat Latte
• Nonfat Latte with Sugar Free Vanilla Syrup
• Iced Nonfat Latte

These are much higher in calcium and protein, and lower in sugar, than the other drink cluster above:

Cluster 11 (Apples)
Here’s a cluster of apples:

• Apple Dippers with Low Fat Caramel Dip
• Apple Slices

Vitamin C, check.

And finally, here’s an overview of all the clusters at once (using a different clustering run):

No More!

I’ll end with a couple notes:

• Kevin Knight has a hilarious introduction to Bayesian inference that describes some applications of nonparametric Bayesian techniques to computational linguistics (though I don’t think he ever quite says “nonparametric Bayes” directly).
• In the Chinese Restaurant Process, each customer sits at a single table. The Indian Buffet Process is an extension that allows customers to sample food from multiple tables (i.e., belong to multiple clusters).
• The Chinese Restaurant Process, the Polya Urn Model, and the Stick-Breaking Process are allsequential models for generating groups: to figure out table parameters in the CRP, for example, you wait for customer 1 to come in, then customer 2, then customer 3, and so on. The equivalent Dirichlet Process, on the other hand, is a parallel model for generating groups: just sample G∼DP(G0,alpha), and then all your group parameters can be independently generated by sampling from G at once. This duality is an instance of a more general phenomenon known as de Finetti’s theorem.

And that’s it.